The Time of Intake to Be Assumed for Calculating DILs and DRLs

DOE-STD-1121-98

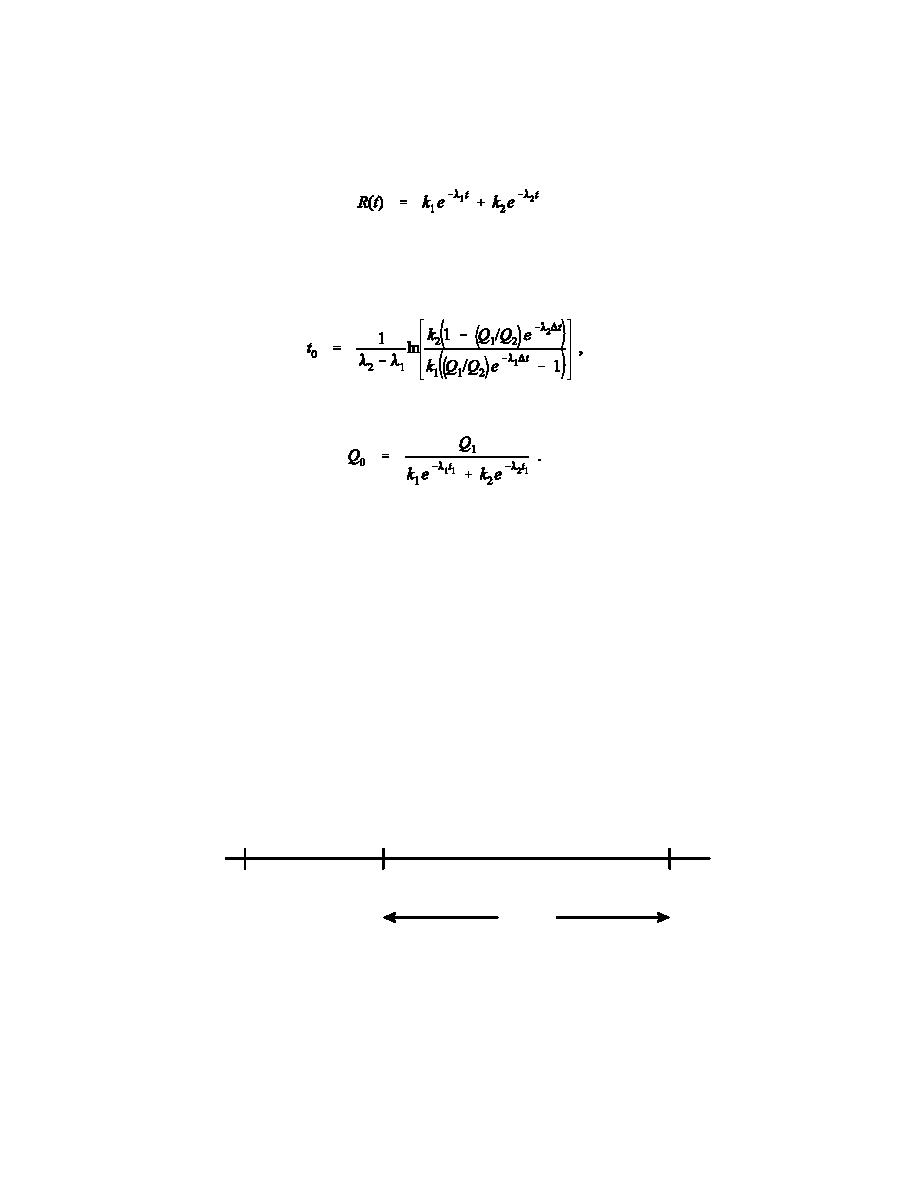
The retention function, R(t), is

(9)

The time of intake, t0, is

(10)

and the retained quantity at t0 is

(11)

For more complex models, analytical solutions are probably not available, but such problems can be

worked out by taking ratios of bioassay results or retained quantities and comparing them to the ratios of

the intake retention functions for the appropriate compartment evaluated at various values of t1 and t1 + )t

values until the correct answer is found. In some cases, there may be two answers; in such cases, other

information, such as three or more bioassay measurements, may be needed to uniquely deduce the time of

intake. The approaches outlined above are meaningful for a single, acute intake. They do not deal with

uncertainties in measured values of Q, which may significantly affect results in some cases. In particular,

these methods are not useful when Q1 and Q2 have similar magnitude and large uncertainties.

7.4.1.2 The Time of Intake to Be Assumed for Calculating DILs and DRLs

DILs and derived reference levels (DRLs) should be calculated at a time of intake that corresponds to

a dose that is the expectation value of dose based on uniform intake probability between bioassay

measurements.

Bioassay 1

Intake

Bioassay 2

(T - ti )

Figure 4. Time Line for Intake Between Two Bioassay Measurements

Let T be the time interval between bioassay samples as shown in Figure 4. Assume that intakes are

equally likely at any time during the interval between bioassay samples, that is, the probability of intake

per unit time is pi(t) = 1/T. Then, the expectation value of time of intake, <ti>, is