Packing Fraction Method - std301320040067

DOE-STD-3013-2004

some alternate methods of estimating the density to be used in the equation must be

developed.

B.3.2.2

Packing Fraction Method

Any powder poured into a container has a bulk density less than the particle density for the

material. Measurements of particle density by gas pycnometer and comparison with bulk density

have shown that the packing fraction, which is the ratio of bulk density to particle density,

varies over a fairly wide range, but does not exceed 0.62 [Mason et al. 1999]. Thus, one

approach would be to determine the bulk density and divide by 0.62, realizing that the true

particle density can be no less than this value (a higher value would result in a smaller volume

occupied by the particles and, hence, a lower theoretical gas pressure). Consequently, if 3.6 kg

of oxide filled a 1.8 l convenience container, the bulk density would be 2.0 kg/l and the

estimated particle density would be 2.0/0.62, or 3.226 kg/l, giving a material volume of 1.116 l.

B.3.2.3

Statistical Method

The packing fraction approach is generally useful only when the bulk density is known. The bulk

density is easily determined if the container is full, but a partially full container makes the

situation more complicated

because of lack of

0.9

knowledge about the volume

0.8

of material. In principle, a

0.7

series of density

0.6

Calcined @ 950

Calcined @ 800

measurements could be

0.5

600, then 950

0.4

Estimated

made to develop a statistical

Bounding

0.3

model of the powder, and

0.2

from that the appropriate

0.1

density could be determined.

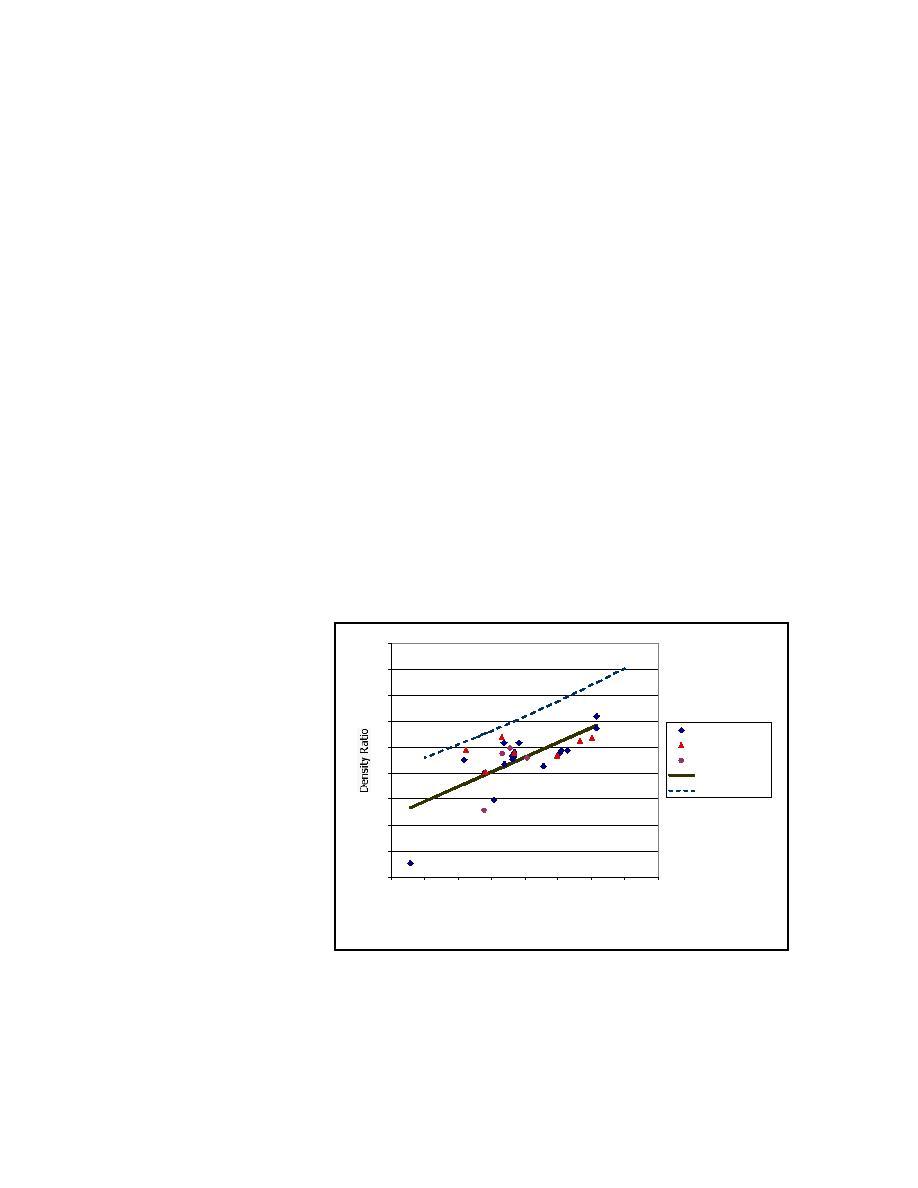
For example, Figure B-2

Bulk Density, kg/l

shows the ratio of bulk

Figure B-2. Statistical model of material density relationship

density to pycnometer

density as a function of bulk density for the materials in the "shelf life" program. The ratios

include material calcined at 950C, 800C, and some that was calcined first at 600C, and then